A. Illustration 1
Consider a netting set with three interest rates derivatives: two fixed versus floating interest rate swaps and one purchased physically settled European swaption. The table below summarizes the relevant contractual terms of the three derivatives. All notional amounts and market values in the table are given in USD. We also know that this netting set is not subject to a margin agreement and there is no exchange of collateral (independent amount/initial margin) at inception.
Trade # Nature Residual maturity Base currency Notional (thousands) Pay Leg (*) Receive Leg (*) Market value (thousands) 1 Interest rate swap 10 years USD 10,000 Fixed Floating 30 2 Interest rate swap 4 years USD 10,000 Floating Fixed -20 3 European swaption 1 into 10 years EUR 5,000 Floating Fixed 50 (*) For the swaption, the legs are those of the underlying swap.
The EAD for un-margined netting sets is given by:
EAD = 1.4 * (RC + PFE)
1. Replacement Cost Calculation
The replacement cost is calculated at the netting set level as a simple algebraic sum (floored at zero) of the derivatives’ market values at the reference date. Thus, using the market values indicated in the table (expressed in thousands):
RC = max {V - C; 0} = max {30 - 20 + 50; 0} = 60
Since V-C is positive (equal to V of 60,000), the value of the multiplier is 1, as explained in the Standards.
2. Potential Future Exposure Calculation
All the transactions in the netting set belong to the interest rate asset class. So the Add-on for interest rate class must be calculated as well as the multiplier since
PFE = multiplier × Add-onagg
For the calculation of the interest rate add-on, the three trades must be assigned to a hedging set (based on the currency) and to a maturity category (based on the end date of the transaction). In this example, the netting set is comprised of two hedging sets, since the trades refer to interest rates denominated in two different currencies (USD and EUR). Within hedging set “USD”, Trade 1 falls into the third maturity category (>5 years) and Trade 2 falls into the second maturity category (1-5 years). Trade 3 falls into the third maturity category (>5 years) of hedging set “EUR”.
S and E represent the start date and end date, respectively, of the time period referenced by the interest rate transactions.
Trade # Hedging set Time bucket Notional (thousands) S E 1 USD 3 10,000 0 10 2 USD 2 10,000 0 4 3 EUR 3 5,000 1 11 The following table illustrates the steps typically followed for the add-on calculation:
Steps Activities 1. Calculate Effective Notional Calculate supervisory duration
Calculate trade-level adjusted notional as trade notional (in domestic currency) × supervisory duration
Effective notional for each maturity category = Σ(trade-level adjusted notional × supervisory delta × maturity factor), with full offsetting for each of the three maturity categories, in each hedging set (that is, same currency)2. Apply Supervisory Factors Add-on for each maturity category in a hedging set (that is, same currency) = Effective Notional Amount for maturity category × interest rate supervisory factor 3. Apply Supervisory Correlations Add-on for each hedging set = Σ(Add-ons for maturity categories), aggregating across maturity categories for a hedging set. One hedging set for each currency. 4. Aggregate Simple summation of the add-ons for the different hedging sets Calculate Effective Notional Amount
The adjusted notional of each trade is calculated by multiplying the notional amount by the calculated supervisory duration SD as defined in the Standards.
d = Trade Notional × SD = Trade Notional × (exp(-0.05×S) – exp(-0.05 × E)) / 0.05
Trade Notional Amount Time Bucket S E Supervisory Duration SD Adjusted Notional d Trade 1 10,000,000 3 0 10 7.869386806 78,693,868.06 Trade 2 10,000,000 2 0 4 3.625384938 36,253,849.38 Trade 3 5,000,000 3 1 11 7.485592282 37,427,961.41 Calculate Maturity Category Effective Notional
A supervisory delta is assigned to each trade in accordance with the Standards. In particular:
- •Trade 1 is long in the primary risk factor (the reference floating rate) and is not an option so the supervisory delta is equal to 1.
- •Trade 2 is short in the primary risk factor and is not an option; thus, the supervisory delta is equal to -1.
- •Trade 3 is an option to enter into an interest rate swap that is short in the primary risk factor and therefore is treated as a purchased put option. As such, the supervisory delta is determined by applying the relevant formula using 50% as the supervisory option volatility and 1 (year) as the option exercise date. Assume that the underlying price (the appropriate forward swap rate) is 6% and the strike price (the swaption’s fixed rate) is 5%.
The trade-level supervisory delta is therefore:
Trade Delta Instrument Type Trade 1 1 linear, long (forward and swap) Trade 2 -1 linear, short (forward and swap) Trade 3 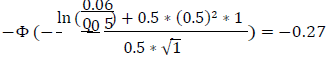
purchased put option The Maturity Factor MF is 1 for all the trades since they are un-margined and have remaining maturities in excess of one year.
Based on the maturity categories, the Effective Notional D for the USE and EUR hedging sets at the level of the maturity categories are as shown in the table below:
Hedging Set Time Bucket Adjusted Notional Supervisory Delta Maturity Factor Maturity category-level Effective Notional D HS 1 (USD) 3 78,693,868 1 1 78,693,868 2 36,253,849 -1 1 -36,253,849 HS 2 (EUR) 3 37,427,961 -0.27 1 -10,105,550 In particular:
Hedging set USD, time bucket 3: D = 1 * 78,693,868 * 1 = 78,693,868
Hedging set USD, time bucket 2: D = -1 * 36,253,849 * 1 = -36,253,849
Hedging set EUR, time bucket 3: D = -0.27 * 37,427,961 * 1 = -10,105,550
Apply Supervisory Factor
The add-on must be calculated for each hedging set.
For the USD hedging set there is partial offset between the two USD trades:
Effective notional(IR) USD = [D22 + D32 + 1.4 x D2 x D3]1/2
= [(-36,253,849)2 + 78,693,8682 + 1.4 × (-36,253,849) × 78,693,868]1/2
= 59,269,963
For the Hedging set EUR there is only one trade (and one maturity category):
Effective notional(IR)EUR = 10,105,550
In summary:
Hedging set Time Bucket Maturity category-level Effective Notional Dj,k Hedging Set level Effective Notional Dj,k (IR) HS 1 (USD) 3 78,693,868 59,269,963
(Partial offset)2 -36,253,849 HS 2 (EUR) 3 -10,105,550 10,105,549.58 Aggregation of the calculated add-ons across different hedging sets:
Effective Notional(IR) = 59,269,963 + 10,105,550 = 69,375,513 (No offset between hedging sets) The asset class is interest rates; thus the applicable Supervisory factor is 0.50%. As a result:
Add-on = SF × Effective Notional = 0.005 × 69,375,513 = 346,878
Supervisory Correlation Parameters
Correlation is not applicable to the interest rate asset class, and there is no other asset class in the netting set in this example.
Add-on Aggregation
For this netting set, the interest rate add-on is also the aggregate add-on because there are no trades assigned to other asset classes. Thus, the aggregate add-on = 346,878
Multiplier
The multiplier is given by:
multiplier = min { 1; Floor+(1-Floor) × exp [(V-C) /(2 ×(1-Floor)×Add-onagg)]}
= min {1; 0.05 + 0.95 × exp [60,000 / (2 × 0.95 × 346,878]}
=1
Final Calculation of PFE
In this case the multiplier is equal to one, so the PFE is the same as the aggregate Add-On:
PFE = multiplier × Add-onagg = 1 × 346,878 = 346,878
3. EAD Calculation
The exposure EAD to be risk weighted for counterparty credit risk capital requirements purposes is therefore
EAD = 1.4 * (RC + PFE) = 1.4 x (60,000 + 346,878) = 569,629